NABS — 桥梁结构非线性分析程序
1 NABS软件功能
NABS为包含空间非线性索单元、桁架单元和梁单元的有限元分析程序,可进行桥梁结构的静力非线性分析和非线性瞬态动力学分析。
NABS的空间索单元性能参见CLS,此处仅展示桁架单元和梁单元。
2 NABS软件功能细节
NABS具有如下具体功能特色:
(1) 空间桁架单元可考虑初应力,并提供初始刚度奇异时的修正策略;
(2) 空间梁单元基于CR模式,可考虑大转动和大位移。
3 NABS软件有效性验证(非线性静力)
以下展示NABS程序非线性静力分析性能的部分验证结果。
3.1 算例L1:集中力作用下的双连杆响应
(1)算例描述
杆件弹性模量为200GPa,截面面积4cm2,计算C点位移和杆件轴力。

本算例验证本程序的桁架单元非线性性能。
(2)算例来源
项海帆等. 高等桥梁结构理论(第二版)[M]. 人民交通出版社, 2013. P359.
(3)计算结果对比
本程序的计算结果对比如表3-1所示。
表3-1 算例L1的计算结果对比
|
项 目 |
精确解 |
本程序结果 |
误差 |
|
位移(cm) |
-0.8846 |
-0.8870 |
0.27% |
|
轴力(kN) |
17.3719 |
17.3263 |
-0.26% |
3.2 算例L2:有初轴力的直杆受竖向力作用
(1)算例描述
杆AB连线长度L=100m,与水平向夹角α=45°,具有初始力T0=71.9208kN,杆件的截面刚度系数EA=1000kN,杆中心C承受竖向集中力P=52.8374kN。计算C点位移和杆件轴力。

本算例验证本程序的桁架单元非线性性能。
(2)算例来源
项海帆等. 高等桥梁结构理论(第一版)[M]. 人民交通出版社, 2001. P248.
(3)计算结果对比
本程序的计算结果对比如表3-2所示。
表3-2 算例L2的计算结果对比
|
项 目 |
文献结果 |
本程序结果 |
误差 |
|
|
位移(m) |
u |
6.55997 |
6.5955 |
0.54% |
|
v |
7.83885 |
7.9670 |
1.63% |
|
|
轴力(kN) |
T1 |
74.9276 |
73.9208 |
-1.34% |
|
T2 |
112.9214 |
111.9208 |
-0.89% |
|
3.3 算例B1:平面坦拱的大变形分析
(1)算例描述
一个两端固定约束的平面圆弧形坦拱,在拱顶作用下一个竖向集中力荷载P。将整个拱分成36个单元,荷载一次性全部加载。
此算例在P=34N和P=36N之间坦拱会出现失稳跳跃现象。因此经常用来检验非线性程序的收敛算法的可靠性。
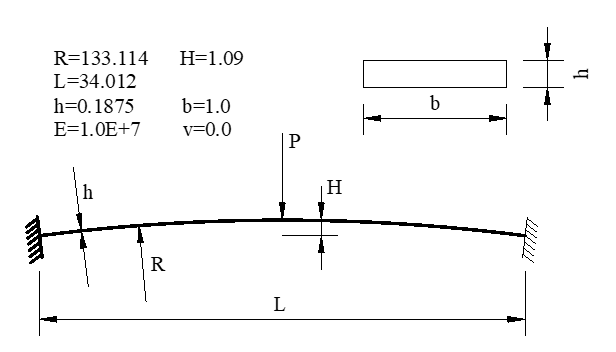
本算例验证本程序的梁单元的非线性性能。
(2)算例来源
丁泉顺,陈艾荣,项海帆. 空间杆系结构实用几何非线性分析[J]. 力学季刊, Vol. 22(3).
(3)计算结果对比
本程序的计算结果对比如表3-3所示。
表3-3 算例B1的计算结果对比
|
P(N) |
本程序计算结果 |
ANSYS计算结果 |
误差 |
|
10 |
3.8423E-02 |
3.8390E-02 |
0.09% |
|
20 |
9.4567E-02 |
9.4283E-02 |
0.30% |
|
30 |
0.2019 |
0.2004 |
0.75% |
|
34 |
0.3319 |
0.3217 |
3.17% |
|
36 |
1.7523 |
1.752 |
0.02% |
|
40 |
1.7775 |
1.7772 |
0.02% |
3.4 算例B2:悬臂曲梁的空间弯扭大变形分析
(1)算例描述
XOY平面内的梁为圆弧形,其半径为100,圆心角为45°。梁一端固定约束,另一端作用有沿Z轴方向的集中力荷载P。将整个拱分成8个单元,荷载一次性全部加载。

此算例为综合性算例,其具有强非线性,经常被用来检验梁单元非线性程序的正确性。
(2)算例来源
丁泉顺,陈艾荣,项海帆. 空间杆系结构实用几何非线性分析[J]. 力学季刊, Vol. 22(3).
(3)计算结果对比
本程序的计算结果对比如表3-4所示。
表3-4 算例B2的计算结果对比
|
P(N) |
位移 |
本程序计算结果 |
ANSYS计算结果 |
误差 |
|
300 |
X |
7.1574 |
7.1139 |
0.61% |
|
Y |
-12.1189 |
-12.165 |
-0.38% |
|
|
Z |
40.4443 |
40.4926 |
-0.12% |
|
|
400 |
X |
9.7698 |
9.7168 |
0.55% |
|
Y |
-16.6698 |
-16.7421 |
-0.43% |
|
|
Z |
46.4391 |
46.5049 |
-0.14% |
|
|
500 |
X |
11.9397 |
11.8825 |
0.48% |
|
Y |
-20.5222 |
-20.6173 |
-0.46% |
|
|
Z |
50.6013 |
50.6798 |
-0.15% |
|
|
600 |
X |
13.7284 |
13.6662 |
0.46% |
|
Y |
-23.7601 |
-23.8765 |
-0.49% |
|
|
Z |
53.6223 |
53.7096 |
-0.16% |
3.5 算例B3:端部弯矩作用下的悬臂直梁
(1)算例描述
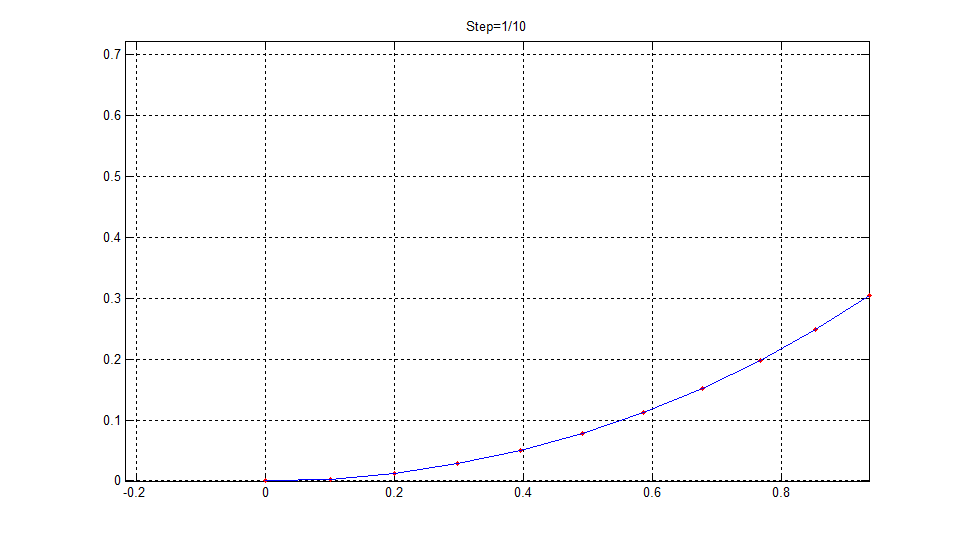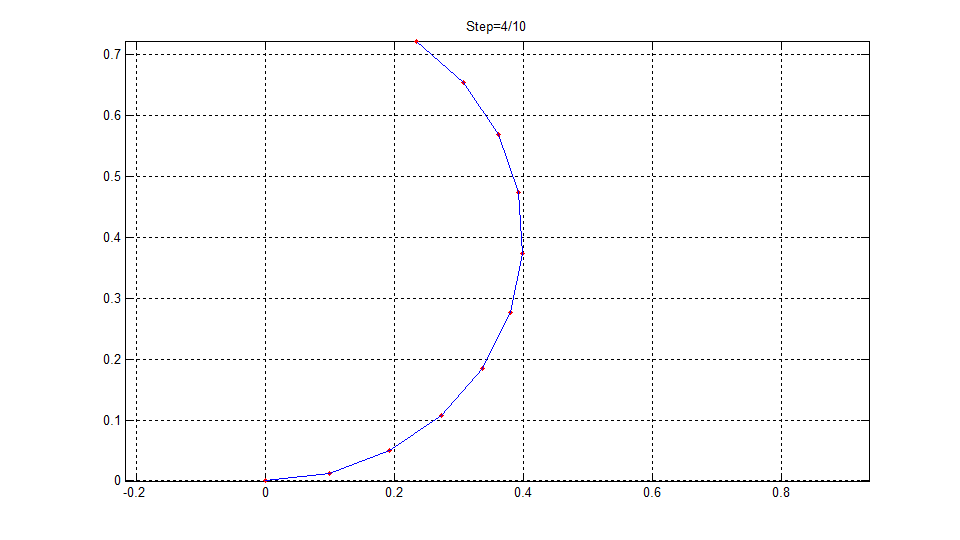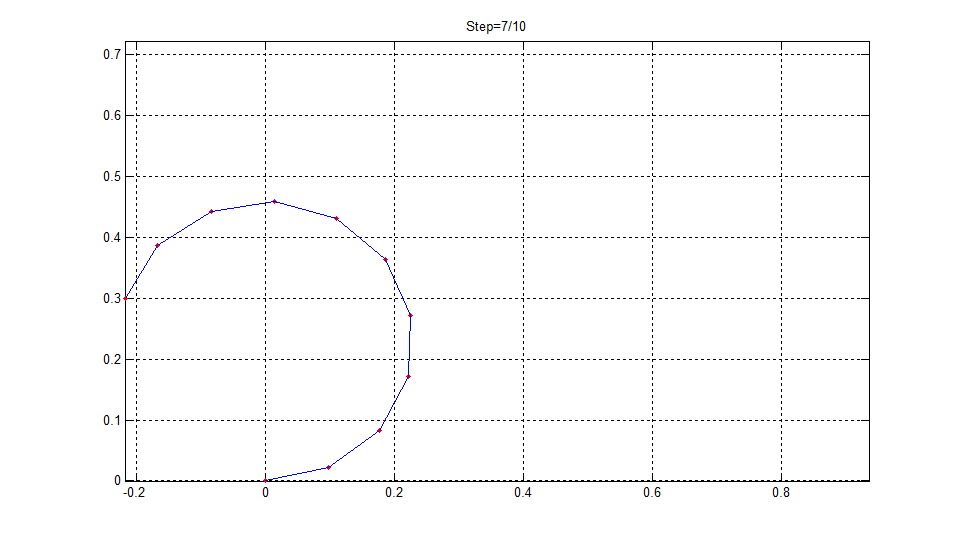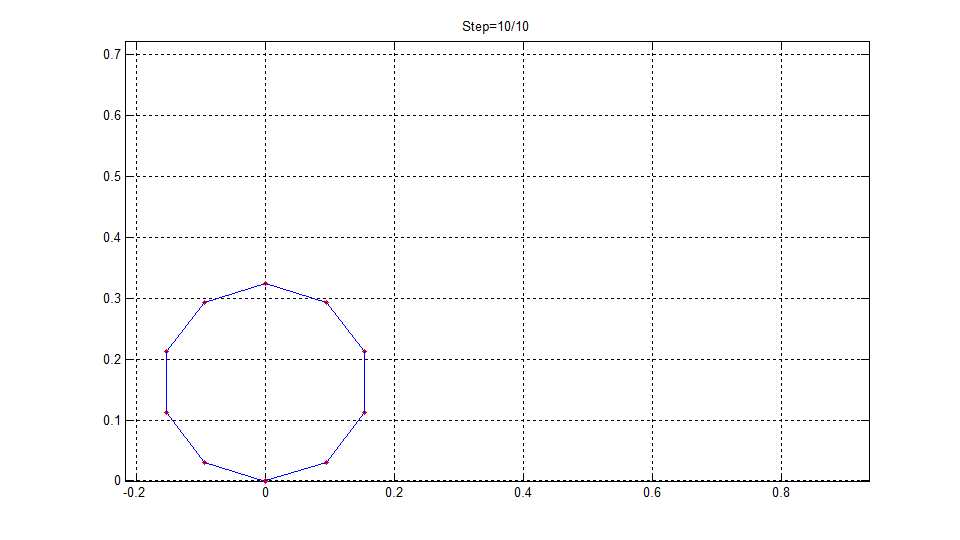
根部固结的悬臂直梁长度L=1m,弹性模量为E=210GPa,截面面积为A=0.01m2,抗弯惯性矩I=8.3333e-6m4。悬臂梁的自由端承受集中弯矩M作用。
当M=2πEI/L时,悬臂直梁将变形为一个圆。
此算例被许多研究者引用来验证程序的大转动能力和数值方法的效率[Hsiao KM, 1987; Crisfield MA, 1990; Lo SH, 1992; 潘永仁,1996; Pai PF, 2000; 陈栋, 2000l; 罗喜恒, 2004]。
将整个梁分成10个单元,荷载一次性全部加载。
(2)算例来源
梁鹏. 超大跨度斜拉桥几何非线性及随机模拟分析[D]. 同济大学博士论文, 2013. P19.
(3)计算结果对比
本程序的计算结果如下图所示,可见悬臂直梁最终变成了一个完整的圆形。
|
|
|
4 NABS软件有效性验证(非线性瞬态动力学)
以下展示NABS程序非线性瞬态动力学分析性能的部分验证结果。
4.1 算例LT1:集中力作用下的双连杆响应
(1)算例描述
杆件弹性模量为200GPa,截面面积4cm2,计算C点集中力突然加载时的C点位移时程。

结构的初始刚度对应的竖弯频率为22Hz,考虑到动力分析时刚度增大,充分地估计竖弯频率为50Hz(周期0.02s),瞬态动力学分析时的积分时间步长取0.001s(Δt=Tn/20)。
(2)不考虑阻尼时
不考虑结构阻尼,设置Rayleigh阻尼系数alpha和beta均为0。
ANSYS中,振幅衰减系数GAMMA设置为0,则对应的Newmark法系数:γ=0.5,β=0.25,此时不包含数值阻尼。
无阻尼时C结点竖向位移时程对比如图4-1所示,可见NABS与ANSYS的结果完全吻合。
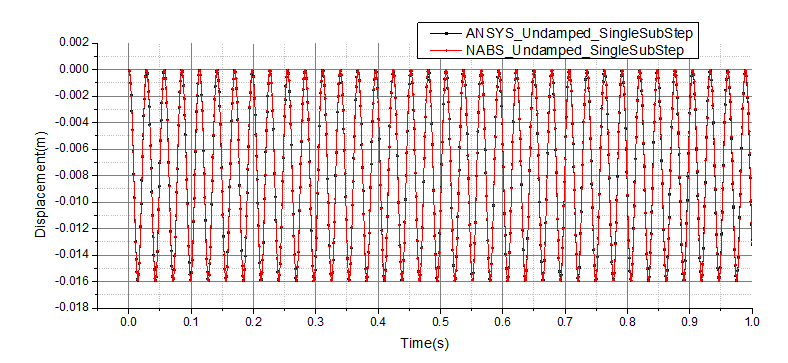
图4-1 算例LT1无阻尼时C点竖向位移时程对比
(3)仅考虑Newmark法数值阻尼时
不考虑结构阻尼,设置Rayleigh阻尼系数alpha和beta均为0。
ANSYS中,振幅衰减系数GAMMA默认为0.005,则对应的Newmark法系数:γ=0.505,β=0.25250625。
仅考虑算法阻尼时C结点竖向位移时程对比如图4-2所示,可见NABS与ANSYS的结果完全吻合。
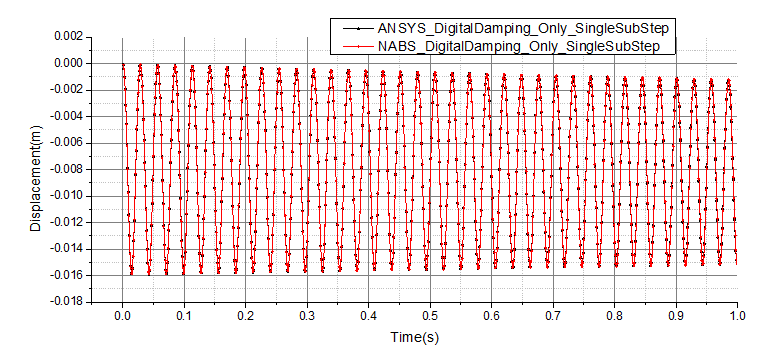
图4-2 算例LT1仅考虑Newmark法算法阻尼时C点竖向位移时程对比
(4)仅考虑Rayleigh阻尼时
ANSYS中,振幅衰减系数GAMMA设置为0,则对应的Newmark法系数:γ=0.5,β=0.25,此时不包含数值阻尼。
阻尼比ksi=0.005,两阶频率均为22.71285Hz,计算得到Rayleigh阻尼常数:α=0.713545,β=0.350363E-04。
仅考虑Rayleigh阻尼时C结点竖向位移时程对比如图4-3所示,可见NABS与ANSYS的结果完全吻合。
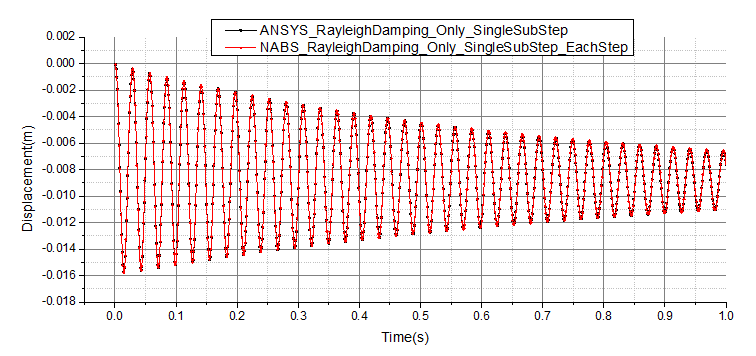
图4-3 算例LT1仅考虑Rayleigh阻尼时C点竖向位移时程对比
(5)同时考虑Newmark法数值阻尼和Rayleigh阻尼时
ANSYS中,振幅衰减系数GAMMA默认为0.005,则对应的Newmark法系数:γ=0.505,β=0.25250625。
阻尼比ksi=0.005,两阶频率均为22.71285Hz,计算得到Rayleigh阻尼常数:α=0.713545,β=0.350363E-04。
同时考虑算法阻尼和Rayleigh阻尼时C结点竖向位移时程对比如图4-4所示,可见NABS与ANSYS的结果完全吻合。
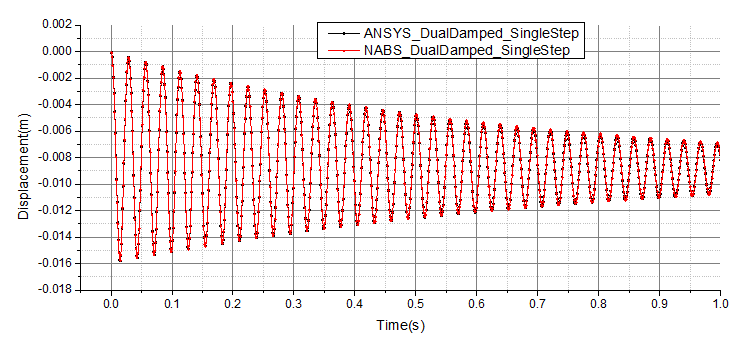
图4-4 算例LT1同时考虑Newmark法算法阻尼和Rayleigh阻尼时C点竖向位移时程对比
4.2 算例BT1:悬臂曲梁的空间弯扭大变形分析
(1)算例描述
XOY平面内的梁为圆弧形,其半径为100,圆心角为45°。梁一端固定约束,另一端作用有沿Z轴方向的集中力荷载P。将整个拱分成8个单元。
计算荷载突然施加到结构上时端部结点的位移时程。

瞬态动力学分析时的积分时间步长取0.02s。
(2)不考虑阻尼时
不考虑结构阻尼,设置Rayleigh阻尼系数alpha和beta均为0。
ANSYS中,振幅衰减系数GAMMA设置为0,则对应的Newmark法系数:γ=0.5,β=0.25,此时不包含数值阻尼。
无阻尼时悬臂梁端部结点竖向位移时程对比如图4-5和图4-6所示,可见NABS与Midas/Civil相对于与ANSYS的结果更加吻合。
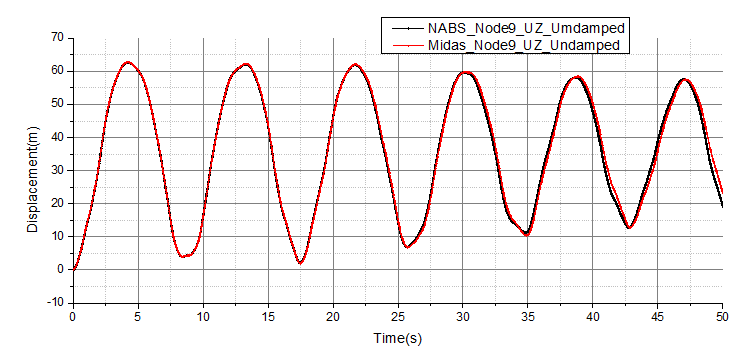
图4-5 算例BT1不考虑阻尼时端部结点竖向位移时程对比(NABS vs Midas/Civil)

图4-6 算例BT1不考虑阻尼时端部结点竖向位移时程对比(NABS vs Midas/Civil,
ANSYS)
(3)仅考虑Rayleigh阻尼时
ANSYS中,振幅衰减系数GAMMA设置为0,则对应的Newmark法系数:γ=0.5,β=0.25,此时不包含数值阻尼。
阻尼比ksi=0.005,两阶频率分别为0.0791Hz和5.2597Hz,计算得到Rayleigh阻尼常数:α= 0.489636E-02,β= 0.298110E-03。
无阻尼时悬臂梁端部结点三向位移时程对比分别如图4-7~图4-9所示,可见NABS与ANSYS的结果吻合较好。
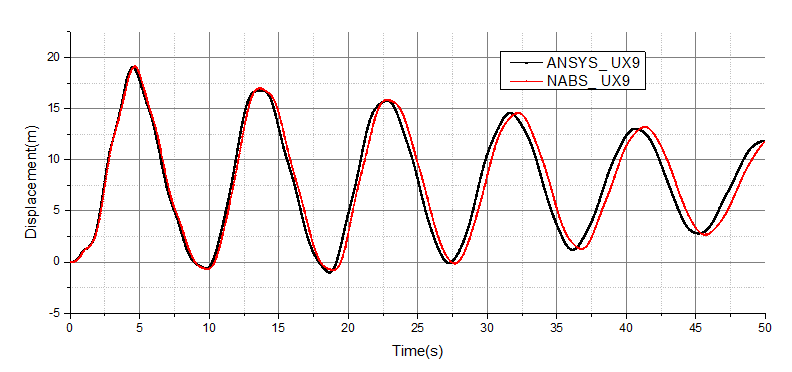
图4-7 算例BT1仅考虑Rayleigh阻尼时端部结点UX位移时程对比(NABS vs ANSYS)

图4-8 算例BT1仅考虑Rayleigh阻尼时端部结点UY位移时程对比(NABS vs ANSYS)

图4-9 算例BT1仅考虑Rayleigh阻尼时端部结点UZ位移时程对比(NABS vs ANSYS)